iSAM2 演算法筆記 (1)：問題定義與 Bayes Tree

圖模型統計推論 (graphical model inference) 應用在 SLAM 問題當中算是行之有年，其中一派由 Kaess 和 Dellaert 等高手開發之 iSAM2 (IJRR 2012) 是一個基於因子圖的最佳化方法，重點是他高度改善了當新增變數到因子圖時的最佳化過程，這件事情使得說由因子圖描述的大型稀疏問題在面對增量變數時，依舊能實現近乎實時的運算效能；同時他們也有釋出 C++ 函式庫。本篇算是筆者對於此方法的回顧，同時也是因為中文的介紹文章比較少，因此也順水推舟地用中文來記錄這個閱讀過程。

前言

對筆者而言，SLAM (Simultaneous Localization and Mapping, 同時定位與地圖構建) 是一個意外有點緣份的題目。第一次是在三、四年前第一次從博班學長口中認識這個名詞；第二次是兩年前，大三仔挑戰碩班課程中稍微碰觸到 EKF-SLAM 和 FastSLAM 的一些技術細節，不到信手拈來，但多少有些基本概念；第三次則是現在，因為目前碩士班的研究方向就是這個部分。

原本以為卡爾曼濾波器 (Kalman filter) 就是 SLAM 問題的解答，但藉由蒐集文獻的過程，以及經過些指點後才意識到：當機器人在行走時，實際上存在 變數跟矩陣維度逐漸上升、缺乏利用稀疏性等問題。以 landmark-based SLAM 而言，除了表自身位姿的變數維度不變之外，地標的數量會隨著移動範圍變廣而增加，因此需要評估的地標數量變多，儘管多數地標通常只對周圍的軌跡有明顯影響，但卡爾曼濾波器在優化過程只能對所有變數進行運算，而忽略了問題本身具備的稀疏性，這件事情比較嚴重的影響在他較難應付大型的場景，畢竟當變數維度突破天際的同時，電腦也要扛不住了。

因此在 SLAM 研究的中後期，大概是十幾年前左右，開始有人轉向用圖優化 (graph-based SLAM) 的方式去處理這個問題：意思是說，我們會把同樣的問題刻劃成一個圖，其中我們把圖的頂點視為變數 (機器人本身的位姿或是地標位置)、邊視為兩個變數之間的相關性 (觀測到的相對位姿或是地標相對位置)。

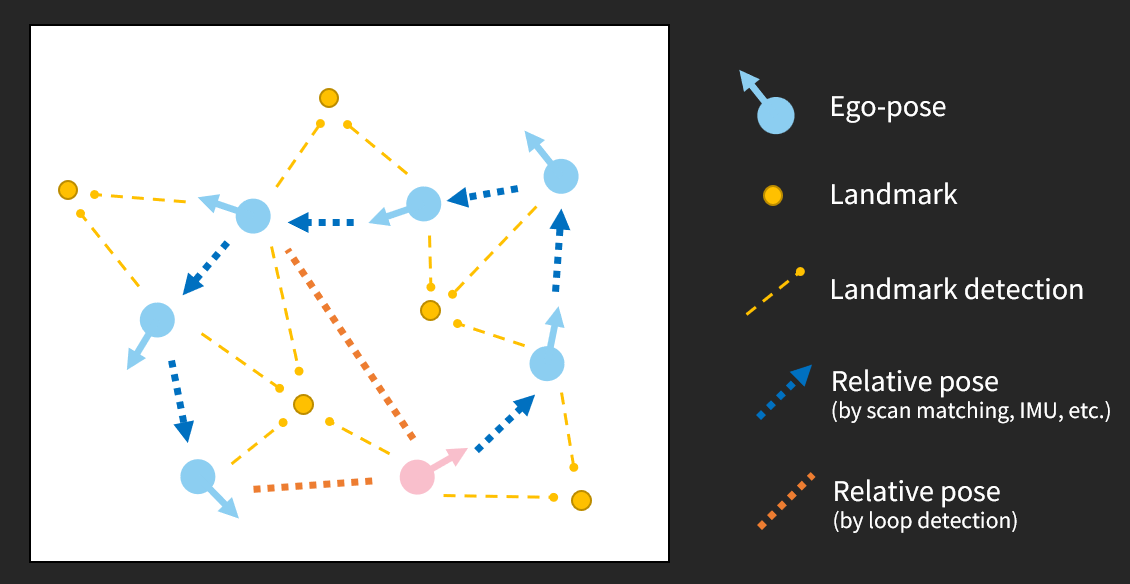
../../../_images/slam-graph-representation.png

SLAM 問題示意圖。其中粉色點代表機器人起始位姿，行徑流程是逆時針繞了一圈後停在起始點之前，其中有五個靜態地標 (十三次地標資訊)、六次連續相對位姿資訊、以及兩次閉迴圈相對位姿資訊。圖是筆者自己畫的。

相較於直接把問題看成是一個超大且稀疏的線性化矩陣，他精準地表達了問題中各個變數之間的關聯性，同時保持了本身的稀疏性。如果用資料結構中圖的觀點來看，有一點 adjacency matrix 與 adjacency list 對照的意味。

Note

實際上 EKF-SLAM 也可以用圖來表達，而基於卡爾曼濾波的方法都需要建立在隱性馬可夫模型 (Hidden Markov Model, HMM) 的假設。

其中我們進一步用因子頂點 (factor node) 去表達變數之間的關聯性，此時一個圖中就同時存在變數頂點 (variable node) 和因子頂點 (factor node)，而所有邊的一端為因子頂點時，另一端必為變數頂點。這個表達方式比起前者更能描繪由多個變數共同組成之關聯性，我們稱這種類型的圖為因子圖 (factor graph)。

Note

儘管在我們的例子中沒有出現由多變數共同決定的因子，但理論上我們是可以這樣玩的。

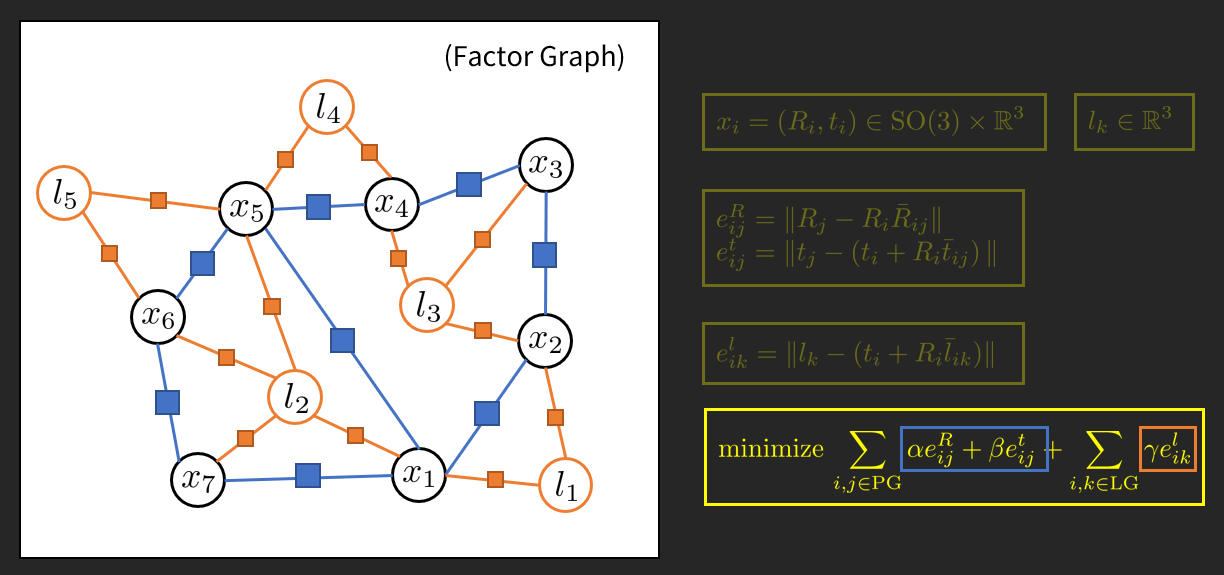
../../../_images/slam-factor-graph.png

使用因子圖表達的 SLAM 問題。其中圓形點代表變數頂點 (variable node)、方形點代表因子頂點 (factor node)。我們先不要陷入圖中一些數學式的細節，重點是先感受前輩們究竟是如何看待這些問題的。圖是筆者自己畫的。

雖然我們把問題描述成一個稀疏的因子圖了，但如果我們還是用通用的演算法 (如 Levenberg–Marquardt algorithm, Gauss-Newton method 等) 逐次去解，那麼就只是換湯不換藥。因此這就是本篇文章的主要重點：透過設計貝式樹 (Bayes Tree) 資料結構以及引進稀疏矩陣分解方法，iSAM2 [isam2] 建構出了一套允許近乎實時計算的稀疏非線性增量最佳化方法 (sparse nonlinear incremental optimization)，並且保障一定程度的計算品質。

問題描述

給定一個因子圖 (factor graph)，實際上他會是一個二分圖 (bipartite graph) \(G = (\mathscr{F}, \Theta, \mathscr{E})\)，其中有

  • 因子節點 (factor node) \(f_i \in\mathscr{F}\),

  • 變數節點 (variable node) \(\theta_j\in\Theta\),

  • 邊 (edge) \(e\_{ij}\in\mathscr{E}\subseteq \Theta\times\mathscr{E}\).

此時我們從因子圖 \(G\) 定義一個目標函數：

\[f(\Theta) = \prod_i f_i (\Theta_i)\]

其中 \(\Theta_i\) 代表與因子節點 \(f_i\) 相鄰的變數節點集合。用機率的觀點來看因子，此時我們會希望得到整體最大機率為目標：

\[\Theta^\star = \mathop{\mathrm{argmax}}_\Theta f(\Theta).\]

以高斯分布作為觀測雜訊模型來說，我們可以把因子節點描述成以下形式：

\[f_i(\Theta_i) \propto \exp\left( \frac{-1}{2} \Vert h_i(\Theta_i) - z_i \Vert_{\Sigma_i}^2 \right),\]

其中 \(h_i(\Theta_i)\) 表觀測函數且 \(z_i\) 表觀測值。這個時候我們將函數帶回最佳化問題，取對數得以下非線性最小平方 (nonlinear least-squares) 問題：

\[\Theta^\star = \mathop{\arg\min}_\Theta \frac{1}{2} \sum_i \Vert h_i(\Theta_i) - z_i \Vert_{\Sigma_i}^2.\]

一般非線性最小平方問題的迭代解法中，在每一次迭代中會對 \(h\) 做線性化 (泰勒級數)，使其變成一個線性最小平方問題：

\[\begin{split}\begin{aligned} \mathop{\arg\min}_\Delta\; (-\log f(\Delta)) &\approx\mathop{\arg\min}_\Delta\; \|H \Delta-\mathbf{z}\|_{\Sigma}^{2} \\ &=\mathop{\arg\min}_\Delta\; (H \Delta-\mathbf{z})^T \Sigma^{-T/2} \Sigma^{-1/2} (H \Delta-\mathbf{z}) \\ &=\mathop{\arg\min}_\Delta\; \| \Sigma^{-1/2} (H \Delta-\mathbf{z}) \|^2 \\ &:= \mathop{\arg\min}_\Delta\; \| A \Delta - \mathbf{b} \|^2. \end{aligned}\end{split}\]

其中 \(H\) 相當於觀測模型的 Jacobian matrix (本身會很稀疏)，\(\Delta\) 則是一個由變數組成的向量。一般來說，當有新的變數 \(\Delta\) 進來的時候，我們會將變數直接串接在 \(\Delta\) 向量的後面 (有點類似增廣矩陣的形式)，只是說如果變數是旋轉矩陣的話，通常會用他的 exponential map (Lie group theory) 去刻劃。

Note

關於旋轉矩陣的變數表達方式，可參考 GTSAM 的官方部落格：Reducing the uncertainty about the uncertainties Part 1, Part 2, Part 3，未來有機會的話筆者再嘗試整理起來。

一般來講，接下來就可以結合一些常見的矩陣分解方法 (e.g. Cholesky or QR factorization) 去找到對應之 normal equation 的解。而 iSAM2 在處理的同時又考慮了變數之間的相依性 (從機率統計的觀點來看就是條件機率)，使得說當讓新變數進來時，對應的最佳化流程不會對全部的 Graph 做計算，而是只針對有關聯的變數做更新。

Bayes Tree

flowchart LR fg[/"Factor Graph"/]:::blue bn[/"Bayes Net"/]:::blue bt[/"Bayes Tree"/]:::blue elimination[Inference and Elimination] creating[Creating the Bayes Tree] fg --> elimination --> bn elimination --> creating bn --> creating creating --> bt classDef gray fill:#ddd,stroke:#444 classDef green fill:#cbecdd,stroke:#42b883 classDef blue fill:#dbedff,stroke:#0c86ff

架構 iSAM2 演算法當中最核心的資料結構就是 Bayes tree，他的特色在於利用樹狀結構表達變數之間的相依性，然而樹狀圖上的點並不是變數，而是 Bayes net 當中的 clique，其中更深層的涵義是序列性條件機率作為樹狀結構的基本單位。因此我們可以把 Bayes tree 理解成是一個某種形式的相依樹。

建構流程上，我們會先透過推論與剪枝 (inference and elimination) 的形式，把一個 factor graph 變成一個相對應的 Bayes net，接著我們會基於 Bayes net 建構出 Bayes tree.

Inference and Elimination (Bipartite Elimination Game)

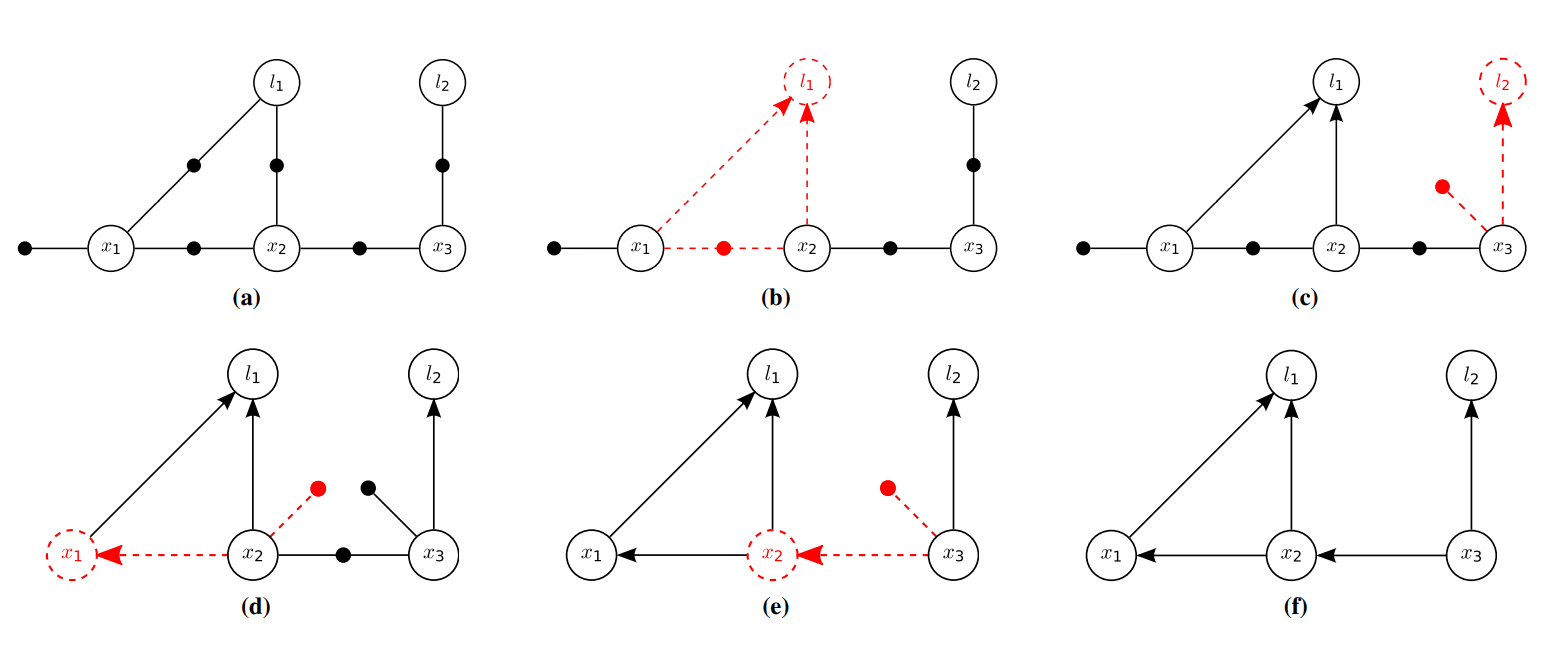
../../../_images/inference-and-elimination.png

從 (a) factor graph 演變為 (f) Bayes net 的分解步驟。在此例當中，依序產生之條件機率是為：(b) \(P(l_1 \vert x_1, x_2)\) (c) \(P(l_2 \vert x_3)\) (d) \(P(x_1 \vert x_2)\) (e) \(P(x_2 \vert x_3)\) (f) \(P(x_3)\)。圖片摘自原始論文。

在 factor graph 這個例子中，這個行為也可以被理解成 Bipartite Elimination Game [bipartite-elimination-game]，不過總而言之，它的核心想法是：逐步將變數節點及其相鄰的因子節點從 factor graph 抽出，並且針對該變數轉換成 Bayes net 的形式 (透過方向表達條件機率的關係)，並且視情況對可能波及到的因子節點做調整。

概念上他的演算法 (從 factor graph 中移除一個變數節點 \(\theta_j\)) 流程如下：

  1. 刪除所有與 \(\theta_j\) 相鄰的因子 \(f_i(\Theta_i)\)，意即： \(\theta_j\in\Theta_i\)，令滿足條件之因子引數集合為 \(I_j\)，並定義 \(S_j=\bigcup_{i\in I_j}\Theta_i\setminus\\{\theta_i\\}\).

  2. 定義 joint density \(f_{\mathrm{joint}}(\theta_j, S_j) = \prod_{i\in I_j} f_i (\Theta_i)\).

  3. 利用機率統計中的 chain rule，得到 \(f_{\mathrm{joint}}(\theta_j, S_j) = P(\theta_j \vert S_j) f_{\mathrm{new}} (S_j)\)，將 conditional density \(P(\theta_j \vert S_j)\) 以單箭頭形式加入 Bayes net，並且將 \(f_{\mathrm{new}} (S_j)\) 視為因子整合到原本的 factor graph.

其中我們討論第二步的實際過程。同樣以 Gaussian 來說，設想一個簡單的狀況 (\(\theta_j\in\mathbb{R}\), \({\boldsymbol{s}}_{j}\in\mathbb{R}^{n_j}\))，我們可以把 joint density 描述成以下形式：

\[\begin{split}\begin{aligned} f_{\mathrm{joint}}(\theta_j, \boldsymbol{s}_j) &\propto \exp \left\{ \frac{-1}{2} \Big\Vert [\boldsymbol{a}_j \vert \boldsymbol{A}_{\boldsymbol{s}_{j}}] \begin{bmatrix} \theta_j \\ \boldsymbol{s}_j \end{bmatrix} - \boldsymbol{b}_j \Big\Vert^2 \right\} \\ &= \exp \left\{ \frac{-1}{2} \Big\Vert \boldsymbol{a}_j\theta_j + \boldsymbol{A}_{\boldsymbol{s}_{j}} \boldsymbol{s}_j - \boldsymbol{b}_j \Big\Vert^2 \right\}. \end{aligned}\end{split}\]

若以 conditional density \(P(\theta_j \vert \boldsymbol{s}_j)\) 的觀點來說，此時把 \(\boldsymbol{s}_j\) 看待為一個非變數，並轉換 conditional density 為以下單變數 Gaussian 的形式：

\[\begin{split}\begin{aligned} P(\theta_j \vert \boldsymbol{s}_j) &\propto \exp \left\{ \frac{-1}{2} \Big\Vert \boldsymbol{a}_j\theta_j - ( - \boldsymbol{A}_{\boldsymbol{s}_{j}} \boldsymbol{s}_j + \boldsymbol{b}_j ) \Big\Vert^2 \right\} \\ &\propto \exp \left\{ \frac{-1}{2} \Big( \color{blue}{(\boldsymbol{a}_j^T \boldsymbol{a}_j)^{-1}\boldsymbol{a}_j^T} \boldsymbol{a}_j\theta_j - \color{blue}{(\boldsymbol{a}_j^T \boldsymbol{a}_j)^{-1}\boldsymbol{a}_j^T}( - \boldsymbol{A}_{\boldsymbol{s}_{j}} \boldsymbol{s}_j + \boldsymbol{b}_j ) \Big)^2 \right\} \\ &:= \exp \left\{ \frac{-1}{2} \Big( \theta_j + \color{blue}{\boldsymbol{a}_j^\dagger}( \boldsymbol{A}_{\boldsymbol{s}_{j}} \boldsymbol{s}_j - \boldsymbol{b}_j ) \Big)^2 \right\} \\ \end{aligned}\end{split}\]

根據以上結果，我們得

\[\begin{split}\begin{aligned} f_{\mathrm{new}}(\boldsymbol{s}_j) &\propto f_{\mathrm{joint}}(-\boldsymbol{a}_j^\dagger( \boldsymbol{A}_{\boldsymbol{s}_{j}} \boldsymbol{s}_j - \boldsymbol{b}_j ), \boldsymbol{s}_j) \\ &= \exp \left\{ \frac{-1}{2} \Big\Vert (\boldsymbol{A}_{\boldsymbol{s}_{j}} - \boldsymbol{a}_j\boldsymbol{a}_j^\dagger\boldsymbol{A}_{\boldsymbol{s}_{j}}) \boldsymbol{s}_j - (\boldsymbol{b}_j - \boldsymbol{a}_j\boldsymbol{a}_j^\dagger\boldsymbol{b}_j ) \Big\Vert^2 \right\} \\ &:= \exp \left\{ \frac{-1}{2} \Big\Vert \color{blue}{\boldsymbol{A}_j'} \boldsymbol{s}_j - \color{blue}{\boldsymbol{b}_j'} \Big\Vert^2 \right\}. \end{aligned}\end{split}\]

其中值得我們關注的特性在於：向量 \(\boldsymbol{a}\_j^\dagger\boldsymbol{A}\_{\boldsymbol{s}\_j}\) 實際上等於對 \(A^T A\) 做 Cholesky factorization 之後，

\[A^T A \overset{\textrm{Cholesky}}{=} R^T R,\]

其上三角矩陣 \(R\) (又稱為 square root information matrix) 的第 \(j\) 個列向量，而此向量在 Bayes net 中又可視為 \(\theta_j\) 所相依的變數指標向量 [bayes-net-textbook]！

這件事情讓我們意識到說：目前在進行的動作，實際上最終的結論就相當於對 \(A^T A\) 做 Cholesky factorization 的結果！

Note

如果我們想對大型線性系統 \(Ax = b\) 求解，一般也會透過解 normal equation \(A^T A x = A^T b\) 的方式去做，此時對 \(A^T A\) 矩陣做 QR 或是 Cholesky 分解，接著就可以透過 backsubstitution 逐步求解。而根據上面的結論，筆者個人的解讀是說： 從 factor graph 轉換成 Bayes net 的過程，在線性代數的觀點就相當於把大型線性系統轉換成 normal equation 的過程。

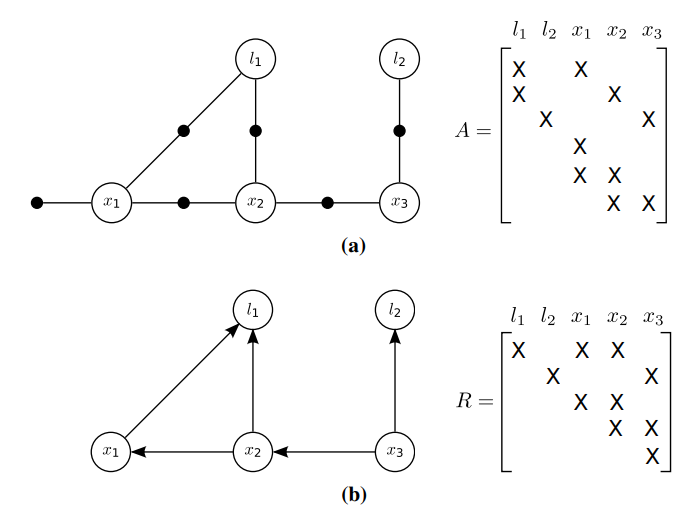
../../../_images/inference-and-elimination-demo.png

從 (a) factor graph 演變為 (f) Bayes net 的示意圖，以及對應的 \(A\) 與 \(R\) 矩陣。圖片摘自原始論文。

Creating the Bayes Tree

透過上述流程所建構出來的 Bayes net，無視方向性的前提下，本身會是一個 chordal graph，而這類的 Bayes net 本身必定存在一種 clique-based tree structure [cowell-probabilistic-networks-and-expert-systems] [mit-ocw-junction-tree-algorithm]，其中樹狀結構的好處在於說他對於相依性的結構表現更為簡潔，而最佳化的過程也會更為簡易。

Note

Chordal graph 的定義是說：一個無向圖中任意四點以上組成的環中必定有弦 (chord)；弦的意思是說：他不是組成環的邊，但他是一個連接其中兩個節點的邊。所以這類的圖又被稱為 triangulated graph.

Note

Bayes net 本身是一個有向無環圖 (directed acyclic graph, DAG)。

這邊所要介紹的是為 Bayes tree：其中邊方向性的概念接近於 Bayes net 中所傳達的條件機率，而節點則是一個潛在的 chordal Bayes net，同時也是一個 clique.

我們將 Bayes tree 的節點 \(C_k\) 用一個條件機率 \(P(F_k\vert S_k)\) 描述之，其中 \(S_k = C_k \cap \Pi_k\) 稱為 separator，\(\Pi_k\) 為 \(C_k\) 的父節點，而 \(F_k = C_k \setminus S_k\) 稱為 frontal variables. 速記為 \(C_k = F_k : S_k\).

此時對應於 Bayes tree 的 joint density 是為

\[P(\Theta) = \prod_k P(F_k \vert S_k),\]

其中對應於根節點的 separator 必為空。

說明完 Bayes net 的形式後，我們說明從 Bayes net 轉換成 Bayes tree 的計算流程。簡單來說是在發掘 clique 的過程中建構而來，從反方向的 elimination 步驟產生之條件機率 \(P(\theta_j \vert S_j)\) 為序，逐項進行以下動作：

  1. 如果 \(S_j = \emptyset\)，初始化一個根節點 (clique) \(C_r = F_r : \\{\\}\)，並跳過以下步驟二和步驟三。

  2. 如果不是，首先找出節點 \(C_p = F_p : S_p\) 滿足 \((S_j)_1 \in F_p\) (雖然 \(S_j\) 是一個集合，但這邊請先當作是一個 sequence 在操作)

  3. 接著，如果 \(F_p \cup S_p = S_j\)，更新該節點為 \(C_p \leftarrow F_p \cup F_j : S_p\)，否則新增一個該節點的子節點 \(C' = \theta_j : S_j\).

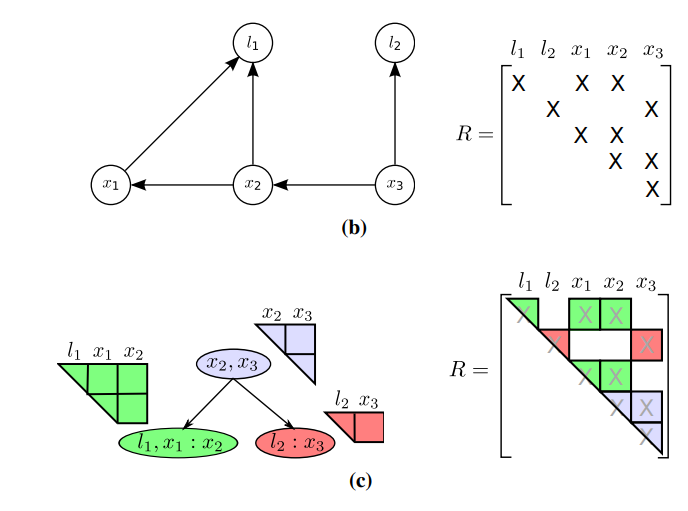
../../../_images/creating-bayes-tree-demo.png

從 (b) Bayes net 演變為 (c) Bayes tree 的示意圖。圖片摘自原始論文。

若以上述圖為例，我們先挖出先前 elimination 步驟所產生的條件機率順序：\(P(l_1 \vert x_1, x_2)\), \(P(l_2 \vert x_3)\), \(P(x_1 \vert x_2)\), \(P(x_2 \vert x_3)\), \(P(x_3)\), 然後反方向開始逐步建構 Bayes tree：

  1. \(P(x_3)\) (條件：\(S_j = \emptyset\))

    graph TD node1(["x3 : {}"]):::blue classDef gray fill:#ddd,stroke:#444 classDef blue fill:#dbedff,stroke:#0c86ff

  2. \(P(x_2 \vert x_3)\) (條件：\(C_p = \\{x_3\\} : \\{\\}\), \(F_p \cup S_p = \\{ x_3 \\} = S_j\))

    graph TD node1(["x2, x3 : {}"]):::blue classDef gray fill:#ddd,stroke:#444 classDef blue fill:#dbedff,stroke:#0c86ff

  3. \(P(x_1 \vert x_2)\) (條件：\(C_p = \\{x_2, x_3\\} : \\{\\}\), \(F_p \cup S_p = \\{x_2, x_3\\} \neq \\{ x_2 \\} = S_j\))

    graph TD node1(["x2, x3 : {}"]):::gray node2(["x1 : x2"]):::blue node1 --> node2 classDef gray fill:#ddd,stroke:#444 classDef blue fill:#dbedff,stroke:#0c86ff

  4. \(P(l_2 \vert x_3)\) (條件：\(C_p = \\{x_2, x_3\\} : \\{\\}\), \(F_p \cup S_p = \\{x_2, x_3\\} \neq \\{ x_3 \\} = S_j\))

    graph TD node1(["x2, x3 : {}"]):::gray node2(["x1 : x2"]):::gray node3(["l2 : x3"]):::blue node1 --> node2 node1 --> node3 classDef gray fill:#ddd,stroke:#444 classDef blue fill:#dbedff,stroke:#0c86ff

  5. \(P(l_1 \vert x_1, x_2)\) (條件：\(C_p = \\{x_1\\} : \\{x_2\\}\), \(F_p \cup S_p = \\{x_1, x_2\\} = S_j\))

    graph TD node1(["x2, x3 : {}"]):::gray node2(["l1, x1 : x2"]):::blue node3(["l2 : x3"]):::gray node1 --> node2 node1 --> node3 classDef gray fill:#ddd,stroke:#444 classDef blue fill:#dbedff,stroke:#0c86ff

Incremental Inference

雖然我們闡述了 Bayes tree 的建構方法，然而須留意的是：上述的建構方法與 Bayes net 的建構順序是相反的，意思是說，當有新的 factor \(f(\Theta)\) 加入系統時，可能會對 Bayes net 的建構順序產生影響，而若我們將以上流程重走一遍，將會導致整個 tree 都需要重建，但這不是我們希望的作法 ── 理想上應該是使用某種編輯機制，使得說只有部分會受到影響的子樹會被改動，而其餘部分依然可以保持不變。

其中我們觀察 Bayes tree 的設計，實際上他反應了 Bayes net 的逆向建構過程：若排除新增的 factor 所引發之條件機率及其後續相關的 Bayes net 建構順序，在這些步驟以前所建構出來的 Bayes net 實際上是不受影響的。這件事情從 Bayes tree 的觀點來看，就是從 root node 沿路到變數集合與 \(\Theta\) 有重疊的 clique node 所形成的 sub-tree 會被更動，而其餘部分則是不受影響。

抱持這個想法，接著我們來看演算法概念就比較容易了 ── 把這些被影響的 sub-tree 重新以 factor graph 的方式描述、加入新的節點、再重新描述成 Bayes tree：給定一 Bayes tree \(\mathscr{T}\) 以及一個新的 factor \(f(\Theta)\)，

  1. 移除受影響的 sub-tree 並重新以 factor graph \(\mathscr{F}'\) 的方式描述

  • 對於任意 clique \(C = F : S\) 滿足 \(F \cap \Theta \neq \emptyset\)，標記從該節點往上直到根節點為須移除之子樹。

  • 統整完後將子樹重新描述成 factor graph，將該樹移除，並且把未移除的數個子樹先儲存起來，稱作 \(\mathbb{T}_\mathrm{orphan}\)。

  1. 將 \(f(\Theta)\) 加入 \(\mathscr{F}'\).

  2. 對於變數節點作重排序 (下一篇筆記的重點之一)。

  3. 根據重排序的結果重新建構對應的 Bayes net 以及 Bayes tree.

  4. 將 \(\mathbb{T}_\mathrm{orphan}\) 以 Bayes tree 的規則安插回對應的位置。

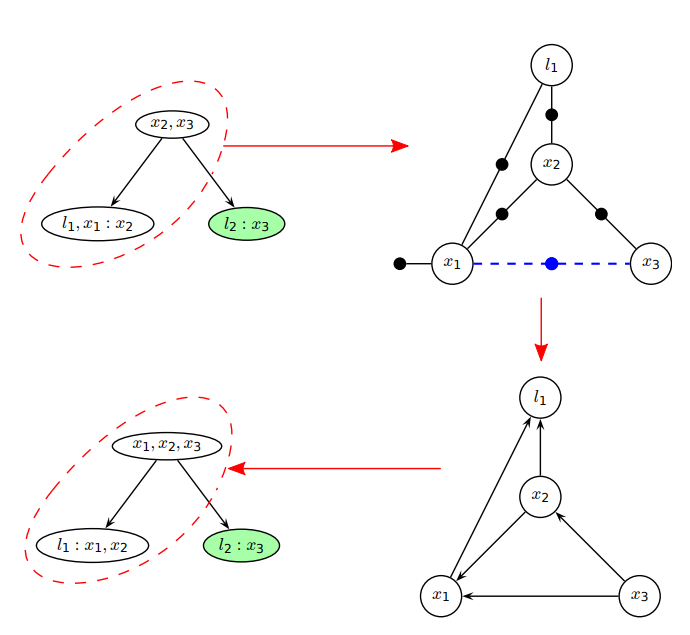
../../../_images/incremental-inference-bayes-tree-demo.png

對 Bayes tree 進行 incremental inference 的步驟示意圖。在本例中所新增的 factor 為 \(f(\{x_1, x_3\})\)，紅色虛線匡列為受影響的子樹，綠色節點則是不受影響的子樹之集合. 圖片摘自原始論文。

到目前為止是簡易的編輯方法，而關於重排序的部分目前還沒有提及。實際上一個好的排序可以讓 Bayes tree 的編輯成本下降，但這部分就留給下一篇再講吧。

結語

我們從一個稀疏的最小平方問題，先是以機率的觀點，用 factor graph 的形式表達後，接著循序引出此篇筆記的重點，Bayes tree 的建構方法。雖然目前還沒有提到，但讀者可以先自行想像，在後續的增量最佳化過程基本上會不斷維護這棵樹，並且以此樹為基礎進行計算。

下一篇筆記的開頭預計會講關於重排序的細節。老實說筆者也不確定需要花多少篇幅才能搞定他們，如果最終太佔篇幅，那麼核心最佳化演算法就會擺到第三篇去 XD

最後提供原作者之一 Kaess 教授在 YouTube 上的相關演講影片、以及該研究團隊開發之公開套件，裡面有包含一些概念和實際應用的例子，筆者覺得都滿值得參考的：

References

isam2

Kaess, M., Johannsson, H., Roberts, R., Ila, V., Leonard, J. J., & Dellaert, F. (2012). iSAM2: Incremental smoothing and mapping using the Bayes tree. The International Journal of Robotics Research, 31(2), 216-235.

bipartite-elimination-game

Heggernes, P., & Matstoms, P. (1996). Finding good column orderings for sparse QR factorization. Department of Mathematics, Linköping University.

bayes-net-textbook

Cowell, R. G., Dawid, P., Lauritzen, S. L., & Spiegelhalter, D. J. (2006). Probabilistic networks and expert systems: Exact computational methods for Bayesian networks. Springer Science & Business Media.

cowell-probabilistic-networks-and-expert-systems

Cowell, R. G., Dawid, P., Lauritzen, S. L., & Spiegelhalter, D. J. (2006). Probabilistic networks and expert systems: Exact computational methods for Bayesian networks. Springer Science & Business Media.

mit-ocw-junction-tree-algorithm

https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-438-algorithms-for-inference-fall-2014/lecture-notes/MIT6_438F14_Lec14.pdf

Context Management in Python   C++ Traits 使用心得

Comments

comments powered by Disqus