
在 Python 基礎科學運算中,我們習於使用 NumPy 以方便且快速地實現矩陣運算,然而在部分情境下仍會遇到效能瓶頸。舉例來說,我們利用 NumPy 線性代數模組處理一個大型線性最小平方問題,但效能瓶頸卻發生在使用原生 Python 迴圈建造矩陣的過程。在本文中,我們將探討 Python 效能瓶頸問題,並試圖使用一些現有工具去達成運算加速的目的,同時比較這些工具之間的特性。
Python 為什麼那麼慢?
Python 好香,但他好慢 🥲
為什麼使用 Python 的理由很簡單,一來他語法親民,能夠快速實現並測試一些功能或者想法;二來他有很多方便、隨裝即用的套件,使用者往往不需要太多的功夫就能達成許多新鮮有趣的程式。
然而眾所皆知, Python 很慢,但也不代表說我們只能乾瞪眼任其一直慢下去。所謂了解問題是解決問題的第一步,不過我們需要分一點層次去探討他慢的理由。以下會用比較簡易的方式進行探討,關於完整的效能議題可以參考 [1]。
Tips
在本文中我們以 CPU-tasks 為主,關於 I/O-tasks 的效能問題則有不同的處理手段。
Python 是動態型別語言
動態型別 (Dynamically typed) 的意思是說,我們不需要為變數指定他的型態,同時我們可以對相同的變數名賦予完全不同型態的值。比如說以下程式碼:
a = 1 # type(a) == int
a = "123" # type(a) == str在第一行時,變數 a 的型態為整數 1,而在第二行時,變數 a 的型態變成字串 "123",且在變數宣告過程中,我們都沒有提示說該變數的型態為何。
相比之下,在靜態型別 (Statically typed) 語言中,像是 C++ 或 Java ,你就必須得這麼做:
int a = 1;
// std::string a = "123"; // You even can't do this
std::string b = "123";如此乍看之下,擁有動態型別特性的語言能帶給我們更大的彈性,並且方便!但是,這個便利性是有代價的。
Python 是直譯型語言
與編譯型 (Compiled) 語言不同的是,直譯型 (Interpreted) 語言會將程式碼編譯成位元組碼 (bytecode),接著再將位元組碼提供給直譯器 (interpreter),讓他轉換成最終的機械碼 (machine code),也就是 CPU 真正看得懂的語言。
這樣乍看下來,在執行階段中,直譯型語言就硬生生比編譯型語言多出了編譯的成本,因為編譯型語言在執行階段就是讀機械碼,不須多加編譯或解析。這個說法本身並沒有錯,但是 Python 慢的主要理由並不只是這裡。一個例子是 Java ,他的編譯過程也是將原始碼轉成位元組碼,並於執行階段再將其交由 JVM 去轉換成機械碼,但 Java 事實上並沒有那麼慢。
真正的問題是動態型別!自由自在的型態使得程式碼的運作行為無法輕易地被預期,因此直譯器必須要逐步執行並逐步判斷接下來的運算行為。就好比程式執行的過程像是火車在前進,在已知型態的前提下,我們可以事先將軌道鋪得遠一些,讓火車不用走走停停的,但 Python 只能讓火車走一步停一步,等軌道鋪好一格後才能繼續走。
到目前為止,我們對於 Python 的效能問題有以下簡單的見解:動態型別的特性逼得 Python 需要設計成直譯型語言,而動態型別的不可預期性讓效能在執行階段難以被優化。
Python 有全域直譯器鎖
Python 使用 reference counting 的方式管理記憶體,並以此作為垃圾回收機制以及記憶體管理的基礎。
這使得說每個變數的計數器在多線程處理中需要被保護,意思是說直譯器需要確保變數在每個時刻下只被一個線程控制 (這意味著新增或者減少參考計數),在 Python 中,他的做法就是引進全域直譯器鎖 (Global Interpreter Lock),強迫在任何時刻下都只有一個線程在運作。
這也是 Python 效能變得不是很優的原因之一,但僅限在多線程處理中才會遇到:本來好端端能平行運算的東西,因為記憶體管理的因素,而被迫降級成實質單線程運算的品質。
Tips
變數的參考計數實際上比你想像中更頻繁得被更動,我們用以下例子說明:
a = 10000000000000000 # import gc; len(gc.get_referrers(a)) == 1
b = a # len(gc.get_referrers(a)) == 2
c = a # len(gc.get_referrers(a)) == 3在程式碼中,第一行宣告變數 a 時,該物件 10000000000000000 會被初始化,並且該計數器為 1 ,當程式執行到第二行時,同樣的物件看似沒有被修改,但他的計數器會加一,因此實質上它的內部數值還是被修改了。
由此可知,第二行跟第三行即使平行化了也不能同步執行,雖然這聽起來很不可理喻,但 Python 就是這樣。
加速符文
到目前為止,我們大致理解 Python 效能問題的主要理由,總算可以來談談如何進行加速了,但這邊還是得先打個預防針:凡好康的福利總是有前提的。
在本文中,我們著重於科學計算 (或者說數值計算) 的加速,為了方便進行不同工具間的比較,我們使用相同的數值計算問題 (弧長計算) 進行演示:給定一個有限數列
我們想要計算出這個數列所形成的弧長
如果用 NumPy 實作這個功能的話,我們可以使用以下程式碼:
# with_numpy/lib.py
import numpy as np
def arc_length(points: np.ndarray) -> float:
"""Compute the arc length of a discrete set of points (curve).
Args:
points (np.ndarray): A list of points.
Returns:
float: Arc length.
"""
piecewice_length = np.linalg.norm(np.diff(points, axis=0), axis=1)
return np.sum(piecewice_length)其中我們將數列表達成一個二維陣列,其中每一列代表數列中的一個點。
其實這個版本跟原始 Python 相比,效能算是還不錯了,不過以下會告訴大家,這還差得遠。
基礎加速符文:靜態型別
儘管 Python 是一個動態型別語言,但其實我們沒有那麼需要動態型別。
就弧長計算的例子來說,我們很明確地知道輸入的數列是一個二維向量,且每一個數值都是符點數,因此我們並不會使用到動態型別的優勢。在這邊我們首先介紹第一個工具 Pythran,他提供了為函數參數提供指定型態的功能,並且將程式碼事先編譯 (ahead of time compilation, AOT) 成可由 Python 於執行階段呼叫的 shared library ,進而達成靜態型別的效益 (同時也省去執行階段編譯的成本)。
# with_pythran/lib.py
import numpy as np
# pythran export arc_length(float64[:, :])
def arc_length(points: np.ndarray) -> float:
"""Compute the arc length of a discrete set of points (curve).
Args:
points (float64[:, :]): A list of points.
Returns:
float: Arc length.
"""
length = 0
for i in range(points.shape[0] - 1):
length += np.linalg.norm(points[i + 1] - points[i])
return length在這邊可以看到我們透過註解 (第四行) 告訴 Pythran 該函數的唯一參數是一個二維的 64-bit 浮點數陣列 float64[:, :],除此之外,你可以看到我們並沒有使用到其他特殊的語句。
接著我們可以使用以下指令進行事先編譯:
pythran lib.py他會在同一層目錄下建立一個名稱類似於 lib.cpython-XXm-x86_64-XXX-XXX.so 的 shared library (在筆者使用的電腦中,該名稱為 lib.cpython-37m-x86_64-linux-gnu.so) ,我們留意到他只能由指定的 Python 版本以及指令集架構呼叫,因為他本身已經是機械碼了。
至此,我們就可以來一窺這個加速符文的功效了:
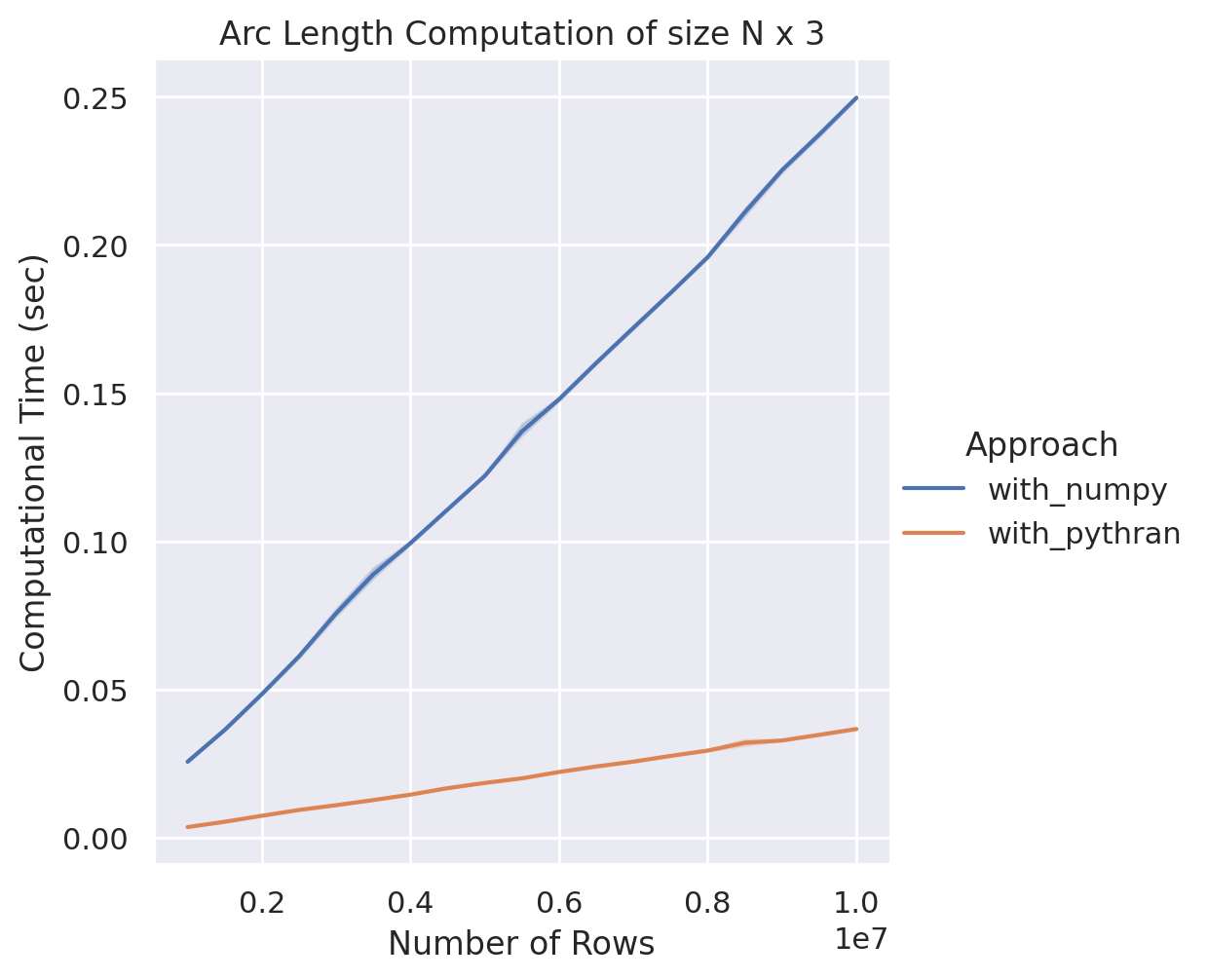
NumPy v.s. Pythran-NumPy
在這個測試當中,我們在固定數值點的維度 (三維) 下,逐步增加點的數量 (在實際測試中我們試驗一百萬到一千萬個點) ,在這之中我們發現在適當的程式編排下, Pythran 的效能比 NumPy 快了約七倍!由此可見,光是固定變數型態,就足以讓編譯器決定說如何能讓程式效率變得更好。
Tips
實際上也有其他套件能做到類似的事情,一個大家常聽到的工具是 Cython,不過使用者需要熟悉 Cython 自定義的語法,他有點像 C/C++ ,但又有些差異。筆者認為他比較難上手,故不在此篇特別做介紹。
Tips
在上文中,所謂「適當的程式編排」指的是說:程式設計師依然要提供正確且簡潔的實作方法,同時也要考量到套件本身對各式語法的支援程度,如此才能將加速機制發揮到極致。
中級加速符文:平行處理
在上述測試中,不管是 NumPy 或者是 Pythran 的初步實作,他們在計算上都是只有使用到單一線程。意思是說,到目前為止的執行效能還可以透過平行化再上一層樓。
幸運的是, Pythran 本身也有提供平行化的功能,在這邊我們需要為本來的程式碼加上 OpenMP 的語法註解。
# with_pythran_omp/lib.py
import numpy as np
# pythran export arc_length(float64[:, :])
def arc_length(points):
"""Compute the arc length of a discrete set of points (curve).
Args:
points (float64[:, :]): A list of points.
Returns:
float: Arc length.
"""
length = 0
# omp parallel for reduction(+:length)
for i in range(points.shape[0] - 1):
length += np.linalg.norm(points[i + 1] - points[i])
return length在以上程式碼中, omp parallel for 是對於 for 迴圈平行化運算的常見起手式,而由於 length 在這個地方是作為累加的單一變數,可能會有所謂的讀寫問題 (readers-writers problems) ,因此我們需要加上 reduction(+:length) 以避免不良的平行化機制。
至此我們再編譯一次,留意我們需要再另外加上 -fopenmp 這個 flag:
pythran -fopenmp lib.py接著我們就可以來看看在平行化加持下的效果如何:
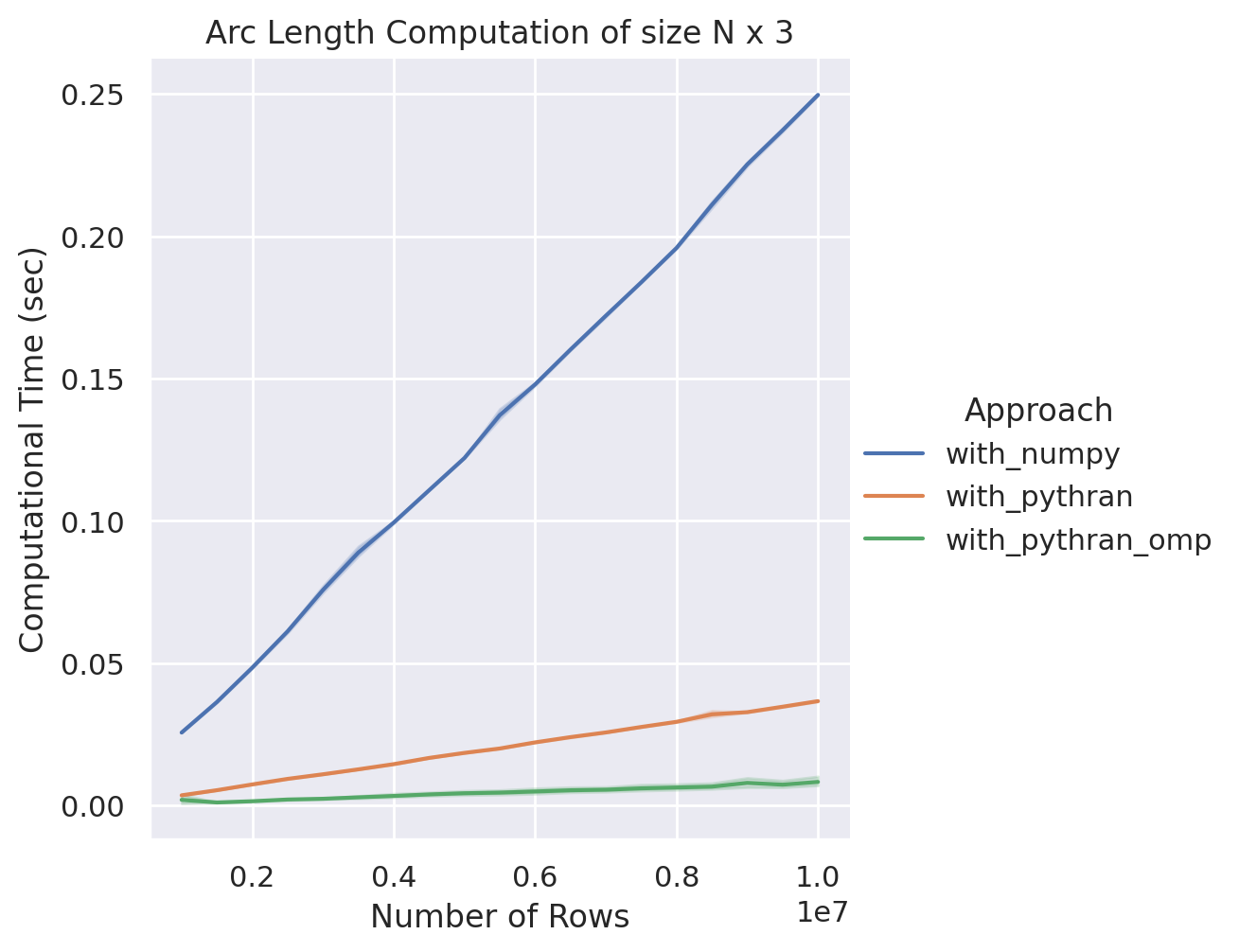
NumPy v.s. Pythran-NumPy (Single) v.s. Pythran-OpenMP (Parallel)
在六核十二執行緒的執行環境下,一樣的測試場景,在一千萬個點的案例中,我們發現在平行化加持下,效能與單執行緒相比又至多能提升四倍左右!並且在這個實作中,我們已經逐漸逼近 CPU 的運算極限了。
此時或許已經有一些讀者開始思考,有沒有稍微簡單一點的平行化方法呢?
答案是有的!我們在此介紹另外一個強大的工具 Numba,他能夠允許使用者在不涉及到這麼多細節的前提下,一樣能達成類似的效果。我們直接上程式碼:
# with_numba/lib.py
import numba as nb
import numpy as np
@nb.njit(parallel=True)
def arc_length(points: np.ndarray) -> float:
"""Compute the arc length of a discrete set of points (curve).
Args:
points (np.ndarray): A list of points.
Returns:
float: Arc length.
"""
length = 0
for i in nb.prange(points.shape[0] - 1):
piecewice_length = np.sqrt(np.sum((points[i + 1] - points[i]) ** 2))
length += piecewice_length
return length在以上實作中,我們利用裝飾器 (Python decorator, @) 對函數進行 Numba 包裝,其中 nb.njit (等價語法為 nb.jit(nopython=True)) 更指定該函數不受 Python interpreter 的介入,使其能夠達到最佳效能。同時我們也指定該函數需要進行平行化,其中我們在第十七行使用 nb.prange 指定該處是可以進行平行化的。
Warning
在 Numba 底層中,他們會自動判斷程式碼並套用合適的平行化機制,不過取而代之,使用者需要透過語法「提示」 Numba 該怎麼做,比如程式碼中的 += 就是一個重要的資訊。詳細的說明可以參考官方文件 [2]。
與 Pythran 不同的是, Numba 透過 just-in-time compilation (JIT) 機制使原始碼在執行階段進行編譯,因此不需要事先編譯。此時我們來看看 Numba 的效果如何:
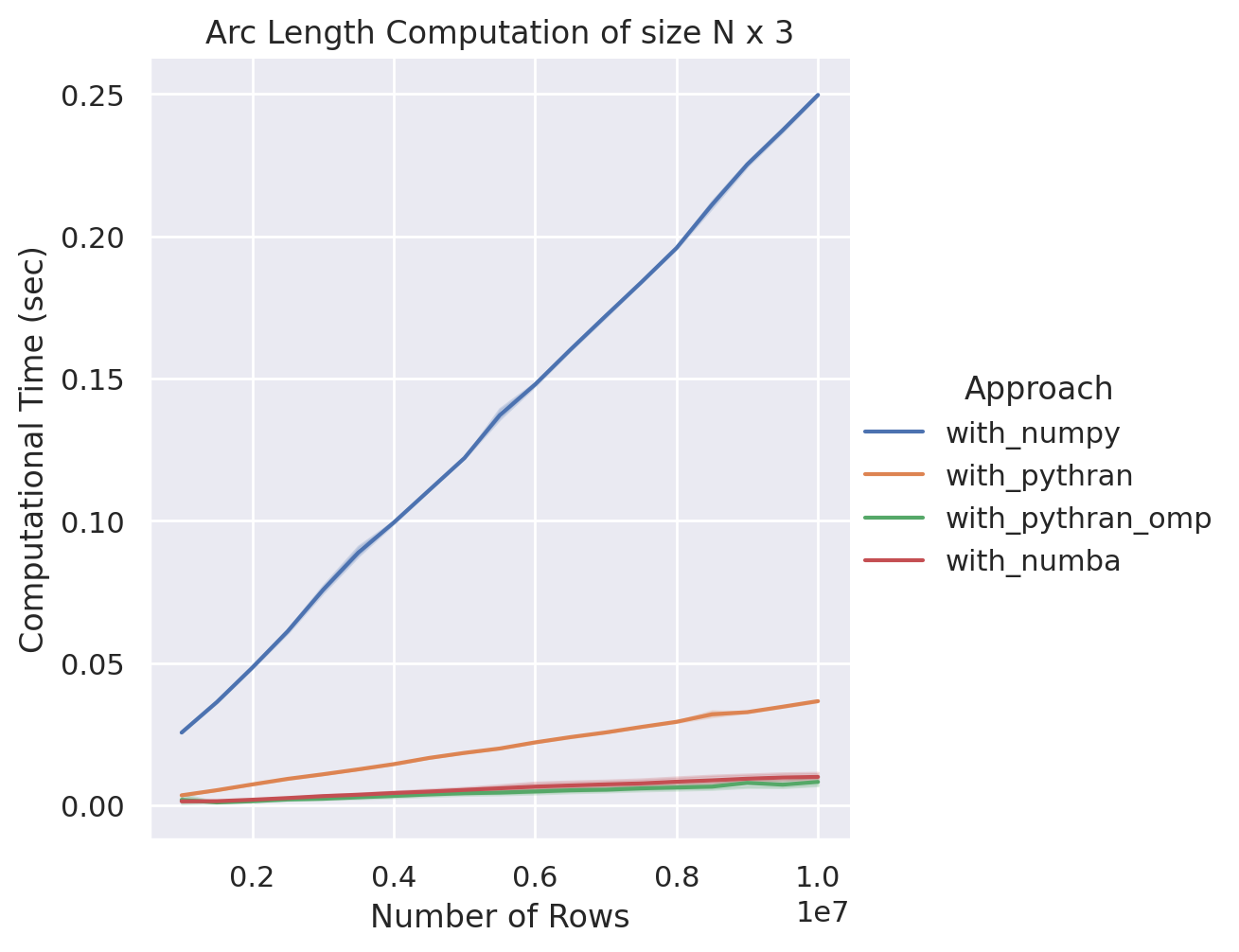
NumPy v.s. Pythran-NumPy (Single & Parallel) v.s. Numba
在這個比較當中,我們發現他與 Pythran 平行化後的效能相比是足以分庭抗禮的,儘管速度上稍微略遜一小截,但我們觀察到 Numba 能夠提供更高階的語法結構,同時可以留意到我們並沒有特別指定變數型態,雖然他還是只能吃 NumPy 陣列,但 Numba 也會根據當下取得的陣列資訊進行優化,藉以獲得更好的執行彈性。
Tips
Numba 還支援基於 CUDA 的 GPU 加速功能 [3] ,因此他也比 Pythran 還具備更多元的加速方案。
Warning
在上述的效能比較中,我們並沒有將 Numba JIT 編譯的時間納入計算,關於這部分的討論我們會放到後面各類工具比較章節討論。
高級加速符文:再見了 Python
從一開始介紹動態型別、GIL 等等的效能瓶頸問題,到後面我們開始探討說:在科學計算中,我們需要動態型別嗎?需要這種記憶體管理機制嗎?而到目前為止的試驗中我們也發現:將這些緊箍咒一一卸下後,我們也獲得了飛躍的效能提升。
此時我們進一步探討:我們真的有那麼需要 Python 嗎?
這句話的意思是說,我們在上述計算成本大的運算中,似乎壓根沒有從 Python 中得到什麼好處,反而是因為 Python 的設計機制導致我們用了不合理的運算時間才能得到計算結果。那有沒有一種可能性是說,我們在上層呼叫中仍然使用 Python ,但在計算部分我們另起爐灶,用更高效能的語言去實作他呢?
此時我們回過頭來提及上述所使用到的兩個工具 Pythran 跟 Numba ,其實他們已經默默幫我們做到這件事情了。
Pythran 本質上是一個 Python-to-C++ 的轉換器,他真正在做的事情是將 Python 程式碼轉換成 C++ 程式碼,再透過 C++ 編譯器編譯成 shared library 供 Python interpreter 使用;而 Numba 則是使用 LLVM 將 Python 程式碼轉換成高效能的機械碼,基本上也是異曲同工。
不過不可諱言地說,他們在使用上還是受到套件本身的限制,比如說 Numba 無法在函數中塞入 NumPy 以外的套件功能 (e.g., Pandas),同時他對於 NumPy 語法的支援也有所侷限,在沒有詳細閱讀文件的前提下直接撰寫也有一定的風險 [4]。而相似的困境在 Pythran 中也會遇到 [5]。
Tips
關於 Numba 的使用注意事項以及心得也可以參考 Jacky 的文章 [6]。
那,我們不妨自己寫 C++ 吧?
其實 NumPy 也是在做類似的事情, NumPy 在內部參照了 CPython API 去實現高性能的科學計算功能,當然我們也可以依樣畫葫蘆,同樣對著 CPython API 刻出我們需要的功能,不過 CPython 在不同版本可能會有不同的 API ,這導致我們在實作上會有一點麻煩。
這邊我們介紹 pybind11,他提供了相對 CPython API 而言更上層的語法介面,讓使用者可以更容易得達成這個目的。到這邊我們就實現真正意義上的使用 C++ 了:沒有奇怪的套件限制,同時可以隨意呼叫任何在 C++ 可以使用的函式庫!
// with_pybind11/src/lib.cpp
#if __INTELLISENSE__
#undef __ARM_NEON
#undef __ARM_NEON__
#endif
#include <pybind11/eigen.h>
#include <pybind11/numpy.h>
#include <pybind11/pybind11.h>
#include <omp.h>
namespace py = pybind11;
int omp_thread_count() {
int n = 0;
#pragma omp parallel reduction(+:n)
n += 1;
return n;
}
double arc_length(Eigen::Ref<Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>> x) {
double length = 0;
omp_set_dynamic(0);
omp_set_num_threads(omp_thread_count());
#pragma omp parallel for reduction(+:length)
for (int i = 1; i < x.rows(); ++i) {
length += (x.row(i) - x.row(i - 1)).norm();
}
return length;
}
PYBIND11_MODULE(lib, m) {
m.def("arc_length", &arc_length);
}在這個範例中,我們使用 Eigen 函式庫實現在 C++ 的線性代數運算,他在 C++ 當中也是相當知名的數學套件,同時學習到上面平行化的精神,我們使用 OpenMP 對各線段長的運算進行平行化處理。
Note
參數型態 Eigen::Ref<Eigen::Matrix<...>> 能夠避免函數呼叫中額外進行不必要的複製 (pass-by-reference),在不使用 Eigen::Ref 的情況下,使用 pybind11 反而可能因為額外的記憶體複製造成效能下降 [7]。
至此,我們對原始碼進行編譯,在這邊我們使用 OpenMP -fopenmp 以及 -O3 編譯優化,最終取得以下效能:
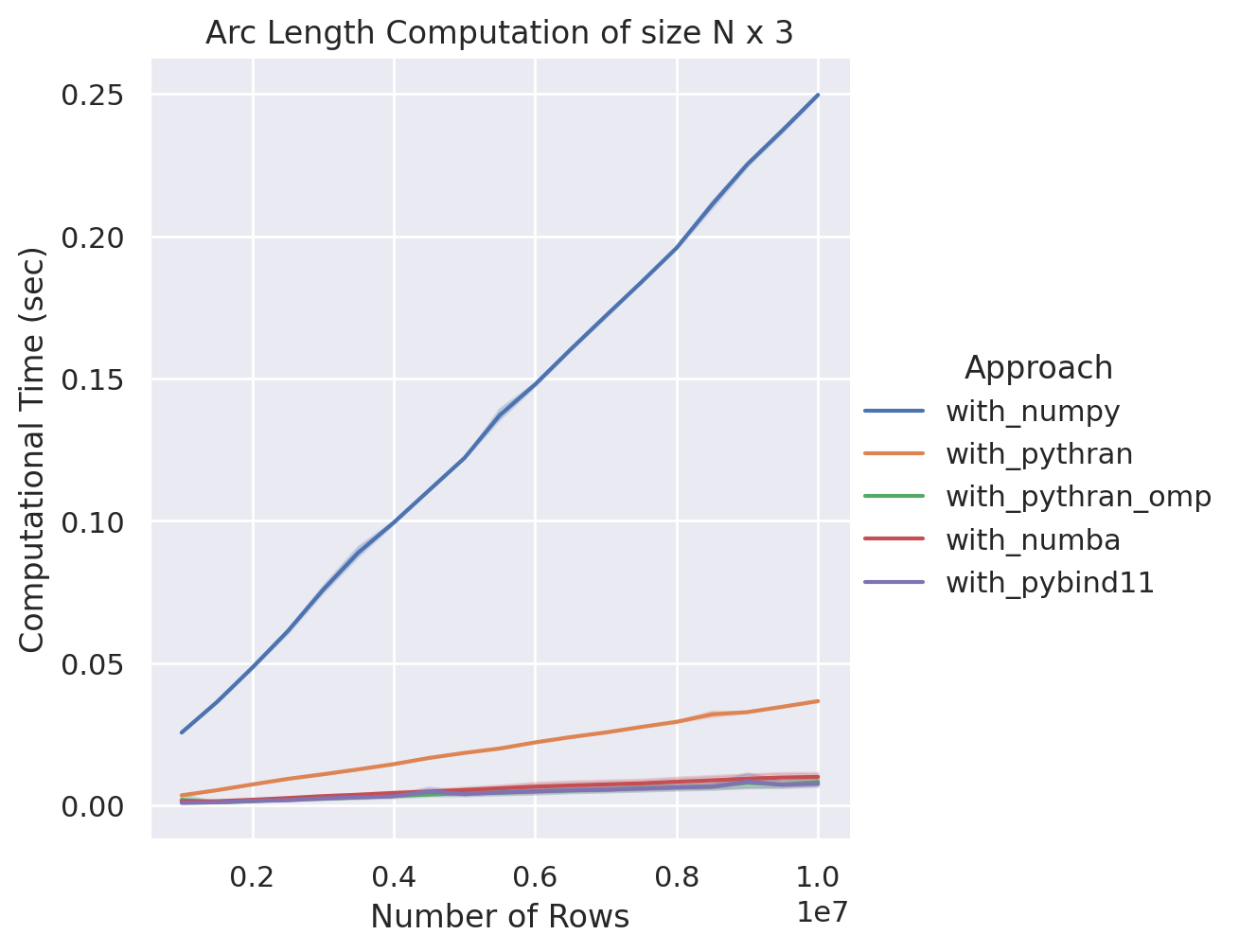
NumPy v.s. Pythran v.s. Numba v.s. pybind11
在這個案例中,我們可以看到 pybind11 與 Pythran 可說不相上下,不過我們切換另一個實驗場景:我們在固定點數量 (一萬點) 的前提下,逐步提升點的維度 (一千維度到一萬維度) ,並比較各方法之間的效能差異:
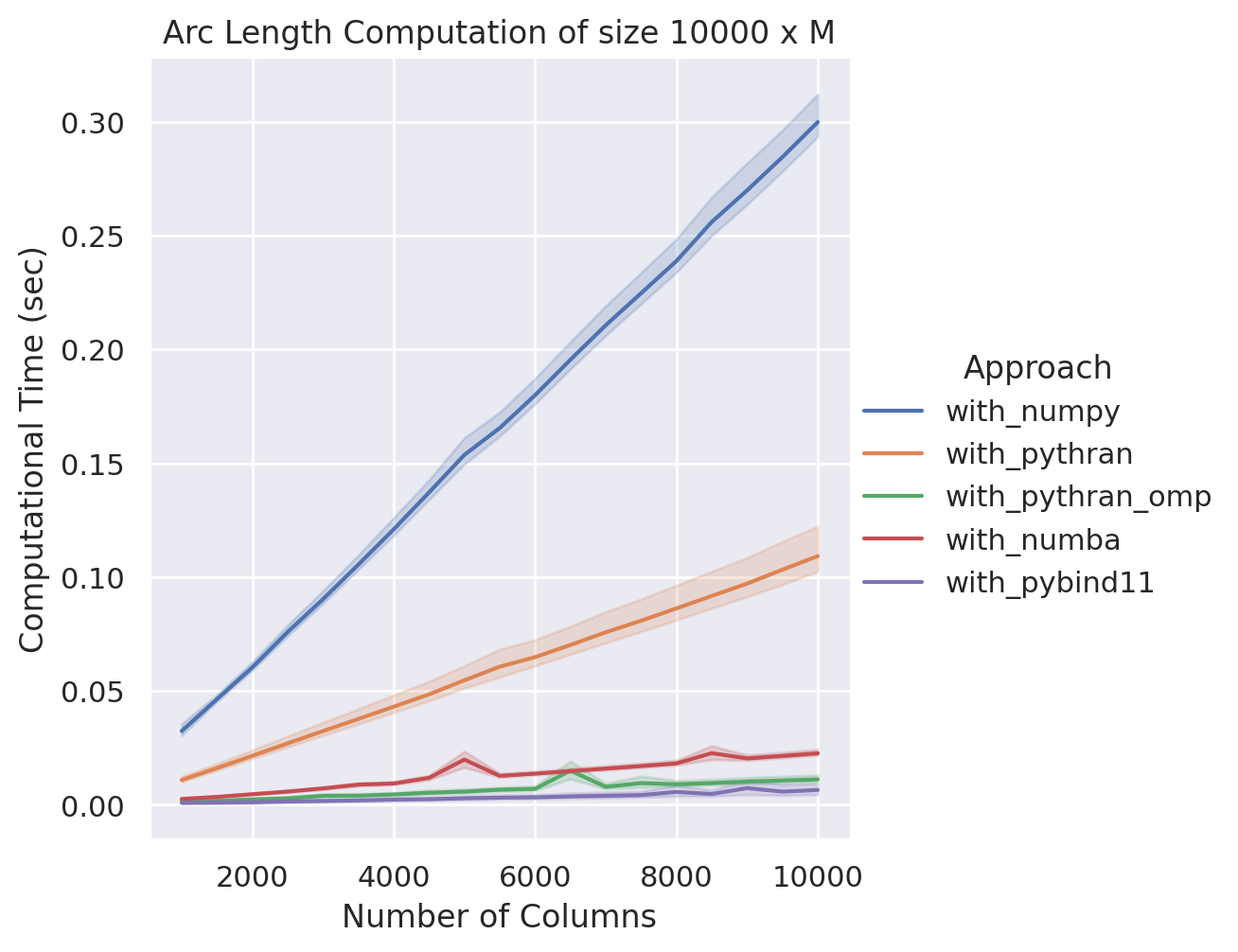
NumPy v.s. Pythran v.s. Numba v.s. pybind11
在這個範例中,我們看到 pybind11 獲得所有方法中最快的效能,在一萬維度的情況下,速度上甚至是第二名平行化 Pythran 版本的兩倍,與原生 NumPy 相比則是快了超過六十倍,至於最原始的 Python 版本我們就別提了。
雖然我們在這個案例中看到了 pybind11 的潛力,但使用這個方法也並非完全沒有缺點。一個明顯的問題是他需要付上一定的成本去建置相關環境,同時也需要考慮顧慮更多的實作細節,以達到最佳的效能。因此在 Python 平行化運算中並不總是提及 pybind11 這個方案,因為他在產品定位上更接近於一個 Python 綁定器 (Python bindings)。
心得
實際上,這些套件他們各自都有自己最關心的議題,故在筆者從開始進行這一系列的測試到現在,並沒有得到所謂「誰才是最佳且唯一解決方案」的結論,而是說我們需要根據當下的實作情境去選擇最適合的工具。因此以下筆者根據自己的使用經驗以及個人感受,提供一個簡易的表格作為套件選擇的依據:
| 套件 | 特色 | 主要限制 | 適用情境 |
|---|---|---|---|
| Cython | Python-to-C/C++ 翻譯器 | 需學習特規語法 | 已熟悉 Cython 語法者較佳 |
| Pythran | Python-to-C++ 翻譯器 | 部分語法不支援 | 想要透過靜態型別實現效能加速,同時可接受較簡易的平行化方案 |
| Numba | 高階科學計算平行化工具 | 部分語法不支援 (少數用法很彆扭)、初次執行需要等待 JIT 編譯 | 想要以不改動過多程式碼的前提下實現平行化加速 |
| pybind11 | C++ 的 Python 綁定器 | 需要熟悉 C++,同時也要考慮記憶體複製問題 | 以 C++ 為套件發展基礎、或者想要追求極致效能、或者單純想炫技 (?) |
| dask | 分散式運算工具,支援大量第三方套件,生態系豐富 | 參數調整不佳的狀況可能導致效能退步 | 需要協同各式套件處理大量資料,或者需要進行叢集運算為佳 |
在表格中我們還另外將 dask 加入比較對象,不過我們沒有將 dask 的效能納入比較對象,除了筆者到目前為止還沒有調出較佳的效能之外,他在使用定位上比較接近叢集運算,這部分就有一點點偏離本篇的主題了,但他仍然是一個非常有趣的套件,若有興趣的讀者可以到他們的官方網站一探究竟。
文末筆者也提供上述測試所使用的 原始碼,若大家閒來無事的話可以參考看看,裡面也有一些本文未提及的暗黑兵法 (例如 CuPy,他是一種 GPU 加速方案),若讀者有相關疑慮或者建議,也非常歡迎在 Issues 或者本篇留言中回覆!
最後,祝福大家能順利幫自己的程式碼套上適合的加速符文囉!
Disclosure
本文封面圖片由 tensor.art 生成。
References
Mike Huls (2021). Why Python is so slow and how to speed it up, Towards Data Science. ↩︎
Numba. Numba for CUDA GPUs. ↩︎
Numba. Supported NumPy features. ↩︎
Pythran. Supported Modules and Functions. ↩︎
pybind11. Pass-by-reference for Eigen. ↩︎